AICとBICの違いとは？モデル評価の基礎をマスターしよう！

今回はモデルの相対比較に使われるAIC(赤池情報量基準)とBIC(ベイズ情報量基準)について解説していきます。

AICとBICは「モデルの複雑さとデータとの適合度のバランス」を評価する相対指標です。モデルの優秀さは、単なる精度の高さだけではなく、汎化性能によっても評価されるからです。

つまりAICとBICは同じ目的に対してどちらがより「モデルの複雑さとデータとの適合度のバランス」が理にかなったモデルであるかを決定する際に使用されます。

Contents

モデルの複雑さとデータとの適合度のバランスとは
AIC(赤池情報量基準)の説明
BIC(ベイズ情報量基準)
最大対数尤度とは
まとめ
実際にやってみよう
- 線形回帰分析
最後に

モデルの複雑さとデータとの適合度のバランスとは

データに適合して良い精度を出すことをデータとの適合度として評価します。精度が良いモデルを評価するのは当然のことなので直感的にも納得できると思います。

その一方でモデルはただ精度が高いほど良いというものではありません。説明変数を大量に使用して複雑な関数としてモデルを作成した場合、訓練データに対して確かに精度は高くなります。しかし、モデルが複雑であるほど訓練データに対して過学習を起こしている可能性が高くなってしまうわけです。また複雑なモデルでは判断の根拠が分かりにくいため解釈性が下がるという問題もあります。これらの理由から複雑であるほど評価を下げると考えるわけです。

そこで重要なのが、モデルの複雑さとデータとの適合度のバランスとなるわけです。以下の例を見てください。

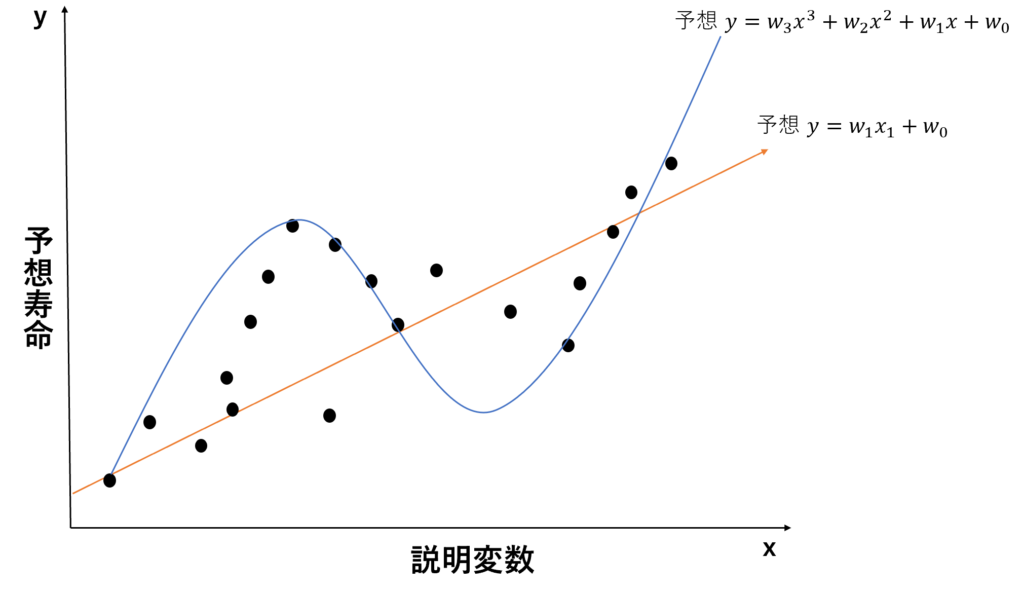
上記の青の予想では、4つのパラメータを使いかなり正解に近い値を出しています。一方で赤の予想では2つのパラメータだけで大雑把に予想していることがわかると思います。この2つを先ほどの観点から見ると、青の予想のほうが、データに適合している一方で赤のほうがモデルは単純であると言うことがわかります。では青と赤ではどちらのほうが優れたモデルなのでしょうか？(xの次数はAICとBICでは関係ないことに注意してください)

これを決定するのがAIC(赤池情報量基準)やBIC(ベイズ情報量基準)です。

AIC(赤池情報量基準)の説明

AICは先ほど説明したように説明変数の組み合わせを相対的に比較するための物でした。ではAICの式を見ていきましょう。AICの式は以下で表されます。

$\text{AIC} = -2\ln(L) + 2k$

$k$はモデルのパラメーター数 $\ln(L)$は最大対数尤度を表します

複数のモデルを比較する際には、AICの値が最も小さいモデルが最適とされます。kはモデルの複雑さを表現した部分です。パラメータの数が増えるとモデルが複雑になるためAICが大きくなるのがわかると思います。

Lはデータにどれほど適合しているかを表した部分です。最大対数尤度というものを使ってデータの適合具合を評価します。最大対数尤度がどのようなものかについて後に説明します。データの適合度が高い程AICが小さくなることがわかると思います。

BIC(ベイズ情報量基準)

BICはAICにさらにサンプル数に関する情報を加えたものです。BICの式は以下で表されます。

$\text{BIC} = -2\ln(L) + k\ln(n)$

BICもAIC同様に小さい値ほど優れている指標です。AICと異なる部分はモデルの複雑さを評価するためにパラメーター数kとサンプル数nの両方を使う点です。複雑なモデルは多くの場合サンプル数も大きくなることからBICはAICに比べてモデルの複雑さに対するペナルティが厳しいと言えます。

最大対数尤度とは

ここではAICとBICで使われているデータの適合度を表す最大尤度について解説します。

尤度とは

ここでは尤度について少し解説したいと思います。尤度とは観測データが特定のモデルのパラメータの下で生成される確率を表現したものです。与えられたデータを90%の確率で生成するモデルは与えられたデータを50%の確率で生成するモデルより優秀なことがわかると思います。

この可能性を求める関数を尤度関数といい下記の式で表されます。

$L(\theta; X) = P(X \mid \theta) = \prod_{i=1}^{n} P(x_i \mid \theta)$

有名な例を挙げます。

今表と裏の確率が平等ではないコインがあります。そのコインを10回投げると表が8回出た後に裏が2回出たとします。するとこの状況下での尤度関数は以下の式になります。

$L(\theta; X) = \theta^8 \cdot (1 – \theta)^2$

$\theta$は今回の場合では表が出る確率です

今この問題に対して2つのモデルを考えます。モデルAは表が出る確率$\theta_\text{A}=0.5$と予想している。モデルBは表が出る確率$\theta_\text{B}=0.9$と予想しているとする

すると与えられたデータは[表、表、表、表、表、表、表、表、裏、裏]という結果を生成する確率は尤度関数より

モデルA$L(\theta; X) = 0.5^8 \cdot (1 – 0.5)^2=0.0009765625$

モデルB$L(\theta; X) = 0.9^8 \cdot (1 – 0.9)^2=0.0043046721$

よって尤度関数からモデルBのほうが優れたモデルであることがわかります。直感的にも表が8回と偏っているため、Bのほうが正しい予想をしてそうだと納得していただけると思います。

このように与えられたデータをモデルが出力する確率を尤度といい、尤度が高いほどデータにモデルが適合していると言えることがわかると思います。

例の場合は離散であったが連続の場合も同様で確率密度関数$P(x)$にデータを代入した場合の積で求められます

対数尤度

尤度関数の対数を取ったものです。以下の式になります。

$\log L(\theta; X) = \sum_{i=1}^{n} \log P(x_i \mid \theta)$

対数をとっても大小関係に変化はなく対数にすることによって積ではなく和で表現できるようにしたものです。単純に計算を便利にするために対数を取ったと考えてください。

最大対数尤度

最大対数尤度とは尤度を最大にするパラメーターのことです。

統計学では、対数尤度の式から対数尤度を最大にするパラメーター$\hat{\theta}$を微分などによって求める必要があります。

一方で機械学習の場合、すでに学習済みのパラメーターがあるため、最大対数尤度を求める必要がありません。AICとBICの計算では学習済みモデル間の比較の場合単に対数尤度を求めればよいということになります。

ここからは細かい話ですが、実は機械学習では学習の過程で尤度を最大にするパラメーターを求めていることが多いです。交差エントロピーを最小化することは対数尤度を最大化することと同義であることは2つの式の関係から明らかになっています。

まとめ

上記のことからAICとBICおいてパラメーター$k$が小さいほうが良い理由と最大対数尤度$\log(L)$がどういったものでなぜ大きい程良いのか分かったと思います

AICとBICはこれら2つのバランスからモデルの性能を評価することで異なるモデル間に優劣を付けより最適なモデルを選択できるようになります。ただし、AICとBICは精度のように絶対的な指標ではないため異なるタスクを目的としてモデル間の比較やモデル単体の評価には使用できないことに注意してください。

実際にやってみよう

線形回帰分析

線形回帰分析の対数尤度の計算方法については以下のように導出できます。

学習済みの線形回帰モデルの式を$y_i = \beta_0 + \beta_1 x_i+ \epsilon_i$とすると($\beta_0 $と$\beta_1 $は学習済みパラメーター)

$\epsilon_i$は残差と呼ばれ正解と予想の差を表します

残差が正規分布であると仮定すると$\epsilon_i \sim \mathcal{N}(0, \sigma^2)$

尤度関数は以下のようになります

$$L(\beta_0, \beta_1, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i – (\beta_0 + \beta_1 x_i))^2}{2\sigma^2} \right)$$

すると対数尤度は以下のようになります

$$\ln L(\beta_0, \beta_1, \sigma^2) = \sum_{i=1}^{n} \left( -\frac{1}{2} \ln(2\pi\sigma^2) – \frac{(y_i – (\beta_0 + \beta_1 x_i))^2}{2\sigma^2} \right)=\ln L(\beta_0, \beta_1, \sigma^2) = -\frac{n}{2} \ln(2\pi\sigma^2) – \frac{1}{2\sigma^2} \sum_{i=1}^{n} (y_i – (\beta_0 + \beta_1 x_i))^2$$

$\sigma^2$は残差の分散であるため計算で求められます

これらのことから説明変数の数を変更してそれぞれのAICとBICを比較してみましょう