今回は勾配を活用した可視化手段であるIntegrated Gradientsについて解説します。Integrated Gradients はGrad-CAM++を改良した手法です。Grad-CAM++と同様に勾配を使用して重要度を計算しますが、勾配の活用方法が大きく異なる手法です。
Contents
Integrated Gradientsとは
従来の勾配ベースの寄与度計算手法(Grad-CAMなど)には、信頼性に関する問題がありました。これらの手法は現在の入力値での局所的な勾配のみを使用するため、以下のような問題が生じます:
- 勾配飽和問題: 重要な特徴でも勾配が0になる領域では寄与度0と判定
- 実装依存性: 同じ機能でも内部構造により異なる寄与度
これらの問題を解決するため、信頼できる寄与度計算手法が満たすべき2つの公理、Sensitivity(感度)と Implementation Invariance(実装不変性)が提唱されました。
Integrated Gradientsは、「基準点から入力点への経路上で勾配を積分する」という新しいアプローチにより、この2つの公理を満たすように設計された手法です。単一点での勾配ではなく、経路全体の勾配情報を統合することで、より信頼性の高い寄与度を提供することができます。
Sensitivity(感度)とは
基準値から現在の入力値の間に、たった1つの特徴だけが変わっていて、その変化によって出力が変化した場合その特徴の寄与度は0であってはならないというルールです。
これは入力として与える特徴のうち1つだけを基準値から現在値まで変化させた場合に出力が変化するならば、その特徴の寄与度が0になってはいけないということです。これは直感的にも納得できる手法だと思います。
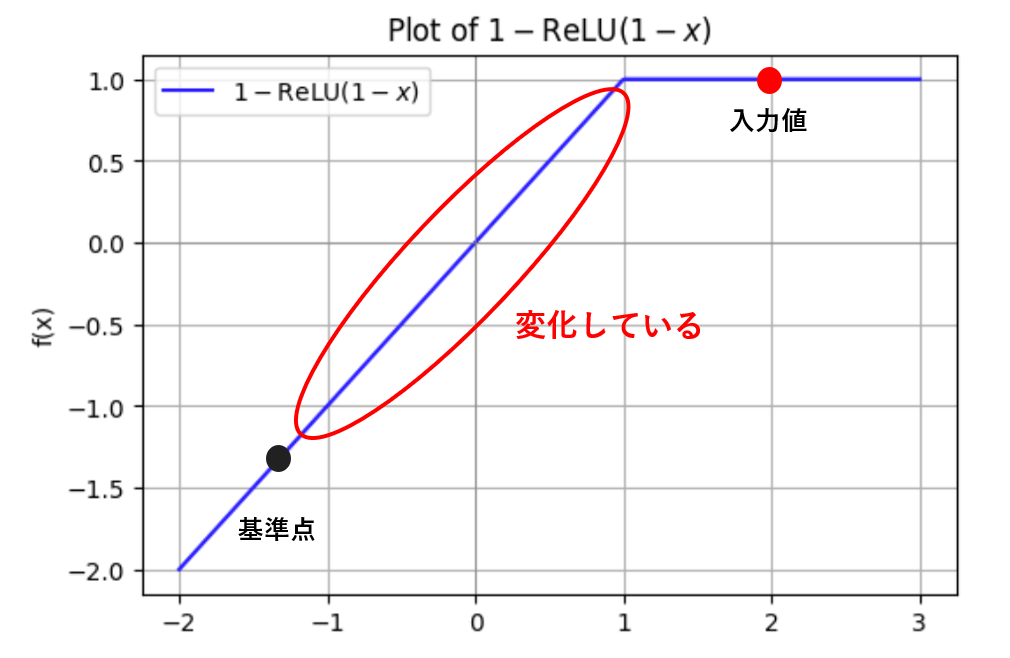
実はGrad-CAMなどはこの公理を満たしていません。その理由としてよく取り上げられるのがReLU関数です。下記の画像は1-ReLU(1-x)のグラフです。xの現在値(入力値)が1以上の場合、ReLU関数の性質上その点での勾配が0となります。よってGrad-CAMではこのxの寄与度を0と判定してしまいます。
しかし実際には、基準値が1以下の領域にある場合、基準値から現在値(1以上)への変化によって出力f(x)は大きく変化します。つまり、このxは実際に出力に影響を与えているのです。
Sensitivityの公理では「実際に出力に影響を与えている変数(特徴)の寄与度は0であってはならない」と定められているため、Grad-CAMのこの判定は公理に反することになります。
実装不変性(Implementation Invariance)とは
実装不変性とは、機能的に等価な2つのネットワークに対して、寄与度計算手法は同じ結果を返すべきであると定義しています。
2つのネットワークがすべての入力に対して同じ出力を返すなら、たとえ内部実装が大きく異なっていたとしても、それらは機能的に等価(functionally equivalent)であると定義されます。実装不変性の公理では、このような機能的に等価なネットワークに対して、寄与度計算手法は同じ結果を返すべきだと要求しています。
この要求が合理的である理由は、入力と出力の関係が完全に同じなら、各入力特徴量が出力に与える影響も本質的に同じはずだからです。もし寄与度が異なってしまうなら、その寄与度計算手法はネットワークの内部実装の違いに惑わされており、関数の本質的な性質を正しく捉えられていないことになります。
つまり、信頼できる寄与度計算手法は、ネットワークの内部構造ではなく、入力と出力の関係のみに基づいて一貫した結果を提供すべきなのです。
実装不変性の具体例
同じ関数でも異なる実装方法が存在する場合を考えてみましょう。例えば、ReLU関数は以下のように複数の方法で実装できます。
実装A(max関数使用):
f₁(x) = max(0, x)実装B(条件分岐使用):
f₂(x) = { x if x > 0
{ 0 if x ≤ 0実装C(絶対値使用):
f₃(x) = (x + |x|) / 2これらの関数は数学的に同じ出力を返します。
実装不変性の公理では、機能的に等価なこれらの関数に対して、寄与度計算手法は同じ結果を返すべきだと要求します。
従来の勾配ベースの手法では、実装時の計算手順や中間変数の設定に依存するため、同じ関数でも実装方法により異なる寄与度が計算される可能性があります。しかし、Integrated Gradientsは積分による計算により、実装方法に関係なく一貫した寄与度を提供します。
一方でGrad-CAMなどは実装不変性を満たしません。Grad-CAMは最後の畳み込み層から出力までの勾配を利用して寄与度を計算します。この性質上、中間層の構造や選択された特徴マップに強く依存するため、ネットワークの内部実装が変わると寄与度の結果も変わってしまうことがあります。
例えば、「Conv1 → Conv2」という二段階の畳み込み処理を行っていたネットワークを考えてみましょう。これをConv1とConv2をまとめてひとつの畳み込み層(Conv*)として再構成した場合:
- 入力に対する最終出力(予測結果)は全く同じ
- しかし、出力される特徴マップの形や性質が変わる
- 結果として、Grad-CAMで可視化されるヒートマップが異なってしまう
これは、モデルが本質的に同じ関数を計算している場合でも、Grad-CAMの説明結果が「畳み込み層の構成」という実装上の違いによって変わってしまうことを意味します。
このように、Grad-CAMはImplementation Invariance(実装不変性)を満たしていないのです。
Integrated Gradientsの仕組み
上記の2つの公理を満たす手法としてIntegrated Gradientsが考えられました。Integrated Gradientsは以下の式で表せます。
| 記号 | 意味 |
|---|---|
| \(x\) | 入力ベクトル |
| \(x’\) | ベースライン(ゼロ入力など) |
| \(x_i\) | 入力ベクトルのi番目の要素 |
| \(F(x)\) | モデルのスカラー出力(例はあるクラスのスコア) |
| \(\alpha \in [0, 1]\) | 補間係数 |
| \(\text{IG}_i(x)\) | i番目の特徴のIntegrated Gradients値 |
Integrated Gradients は、入力の各特徴量(たとえば画像の各ピクセル)が、モデルの出力にどの程度影響を与えているかを測るための手法です。
この手法では、入力値を真っ黒な画像から徐々に現在の入力値へと連続的に変化させ、その過程において出力の勾配を観察します。そして、全体にわたってそれらを積分することで、出力に対してどれだけ貢献したか(寄与度)を正確に計算します。勾配を取るというところは同じですがこの方法は上記の2つの公理を満たしています。
Integrated GradientsがSensitivity(感度)を満たす理由
まず1つ目の公理であるSensitivity(感度)について説明します。今回は画像を扱うため、各ピクセルの値は0〜255の範囲に限定されています。これを0〜1の範囲に正規化することで、基準点から入力画像までのすべての中間状態を線形補間し、その経路上での勾配を積分して寄与度を求めることが可能になります。
これは、入力を基準となる値(たとえば真っ黒な画像 ピクセルの値が0)から、目的の画像(ピクセル値が正規化されて [0,1] 範囲にある)まで線形に変化させることで、各ピクセルがどの程度出力に影響を与えているかを滑らかに測るという考えに基づいています。ここで、ピクセルの値の変化によって結果に差が生じた場合には、どのような経路の関数であろうとも積分結果は0になりません。このことからIntegrated GradientsはSensitivity(感度)を満たしていると言えます。
Integrated Gradientsが実装不変性(Implementation Invariance)を満たす理由
Integrated Gradientsは積分による計算を行うため、実装不変性を満たします。同じ入出力を持つ関数ならば、内部構造にかかわらず積分結果は必ず同じになります。よって、関数の内部実装によってIntegrated Gradientsは変化しないため、実装不変性を満たします。
Integrated Gradientsの実装と実験結果
以下はIntegrated Gradientsを実装したコードとその実行結果です。今回はResNetというモデルが犬と分類した画像に対してその判断根拠を可視化させました。CAMやGrad-CAM++などと比べると非常に細かくややわかりにくい印象を受けました。Grad-CAMなどの手法は畳み込み層に対して処理を行う性質上ある程度まとまった範囲が強調されますが、Integrated Gradientsは1ピクセルごとに処理を行うため、かなり細かい結果になります。この手法は1ピクセルごとに独立して処理を行うため、ピクセル間の関係をやや無視した手法になっていることも原因の1つであると考えられます。
import numpy as np
import tensorflow as tf
import cv2
import matplotlib.pyplot as plt
from tensorflow.keras.applications.resnet50 import ResNet50, preprocess_input, decode_predictions
# モデルロード(学習済み ResNet50)
base_model = ResNet50(weights="imagenet")
model = tf.keras.models.Model(inputs=base_model.input, outputs=base_model.output)
# 画像前処理
def preprocess_image(image_path, target_size=(224, 224)):
img = cv2.imread(image_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img = cv2.resize(img, target_size)
img = img.astype(np.float32)[None, ...] # (1, 224, 224, 3)
img = preprocess_input(img)
return img
# Integrated Gradients 計算
def integrated_gradients(model, input_tensor, target_class_index, baseline=None, steps=200):
if baseline is None:
baseline = np.zeros_like(input_tensor).astype(np.float32)
input_tensor = tf.convert_to_tensor(input_tensor, dtype=tf.float32)
baseline = tf.convert_to_tensor(baseline, dtype=tf.float32)
total_gradients = tf.zeros_like(input_tensor[0])
for alpha in np.linspace(0, 1, steps):
x_interp = baseline + alpha * (input_tensor - baseline)
x_interp = tf.convert_to_tensor(x_interp, dtype=tf.float32)
with tf.GradientTape() as tape:
tape.watch(x_interp)
pred = model(x_interp)
target = pred[:, target_class_index]
grads = tape.gradient(target, x_interp)[0]
total_gradients += grads
avg_grads = total_gradients / steps
ig = (input_tensor[0] - baseline[0]) * avg_grads
# ヒートマップ化
ig_map = tf.reduce_sum(tf.math.abs(ig), axis=-1).numpy()
ig_map = (ig_map - ig_map.min()) / (ig_map.max() - ig_map.min() + 1e-8)
ig_map = np.clip(ig_map * 4.0, 0, 1)
return ig_map
# ヒートマップ合成
def overlay_ig(image_path, ig_map, alpha=0.5):
raw_img = cv2.imread(image_path)
raw_img = cv2.cvtColor(raw_img, cv2.COLOR_BGR2RGB)
H, W, _ = raw_img.shape
heatmap = cv2.resize(ig_map, (W, H))
heatmap = (heatmap * 255).astype(np.uint8)
heatmap_color = cv2.applyColorMap(heatmap, cv2.COLORMAP_JET)
heatmap_color = cv2.cvtColor(heatmap_color, cv2.COLOR_BGR2RGB)
overlay_img = cv2.addWeighted(raw_img, 1 - alpha, heatmap_color, alpha, 0)
return raw_img, overlay_img
# メイン実行
if __name__ == "__main__":
image_path = "" # ←ここを画像パスに変更
# 画像の予測
input_img = preprocess_image(image_path)
preds = model.predict(input_img)
top_pred_index = np.argmax(preds[0])
decoded = decode_predictions(preds, top=5)
print("Top-5 Predictions:")
for (imagenet_id, label_name, score) in decoded[0]:
print(f"{imagenet_id} : {label_name} (score={score:.4f})")
# IG計算と可視化
ig_map = integrated_gradients(model, input_img, target_class_index=top_pred_index, steps=200)
raw_img, ig_img = overlay_ig(image_path, ig_map, alpha=0.5)
# 結果表示
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(raw_img)
plt.title("Original Image")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(ig_img)
plt.title("Integrated Gradients")
plt.axis("off")
plt.show()

まとめ
今回はモデルの判断根拠の解析に使用される Integrated Gradients について解説しました。この手法を考案した筆者たちは、モデルの判断を解釈する上で多くの問題が未解決であることを認めつつも、「何が出力にどれだけ寄与したのか」を理論的に正当な形で捉える一歩として、この手法を提案しています。
彼らは特に、アトリビューション(寄与度)の信頼性を評価するための基準(公理)が必要であると主張し、感度(Sensitivity)と実装不変性(Implementation Invariance)という2つの公理を導入しました。Integrated Gradients はこの2つの公理をともに満たしており、勾配ベースのシンプルな仕組みにも関わらず、堅牢な可視化と解析が可能です。
ただし著者らは同時に、「入力特徴間の相互作用」や「ネットワークがどのような論理で判断しているのか」といったより深い構造的理解についてはまだ課題が多く、モデルの内部を完全に“理解する”ことはまだ難しい段階にあると述べています。













