リカレントニューラルネットワークとは、時系列データやシーケンシャルデータに特化したモデルであり、時系列を考慮した解析を可能とするモデルです。リカレントニューラルネットワークの代表的なモデルであるLSTMなどはご存じの方も多いのではないでしょうか。今回はそんなリカレントニューラルネットワークの中でも最も基本的なモデルである単純リカレントニューラルネットワークについて解説しました。
リカレントニューラルネットワーク(RNN)とは
リカレントニューラルネットワークは時系列を考慮した機械学習モデルです。具体的には、判断材料として前の状態を考慮して判断を行う設計になっています。その構造によって、前の時系列の判断が重要となるタスクに強いモデルとなっています。
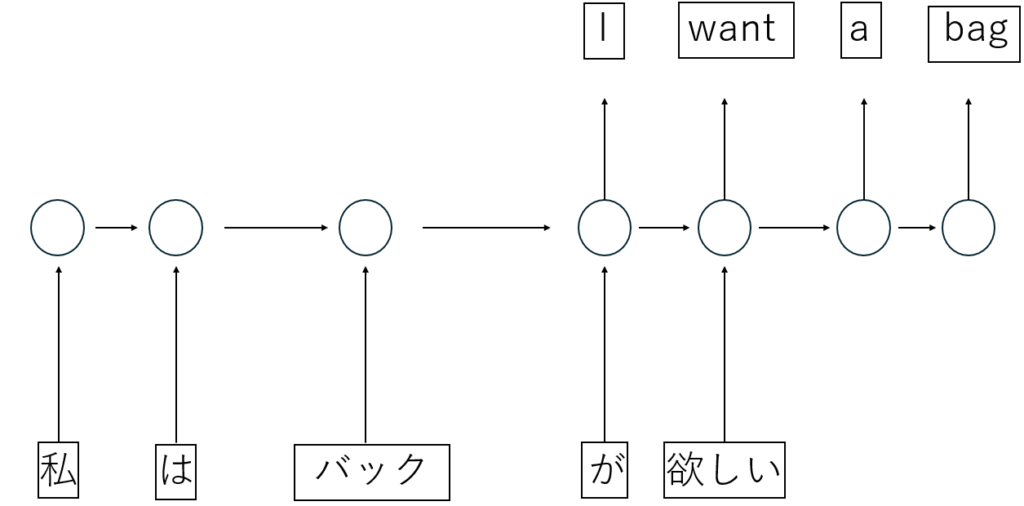
例えば、上記の画像のような翻訳タスクなどは過去の入力を考慮した翻訳が必要となるため、RNNなどが適しているとされていました。また株価予測や音声データ解析も時系列データであるためRNNが得意とするタスクです。
リカレントニューラルネットワーク(RNN)の構造
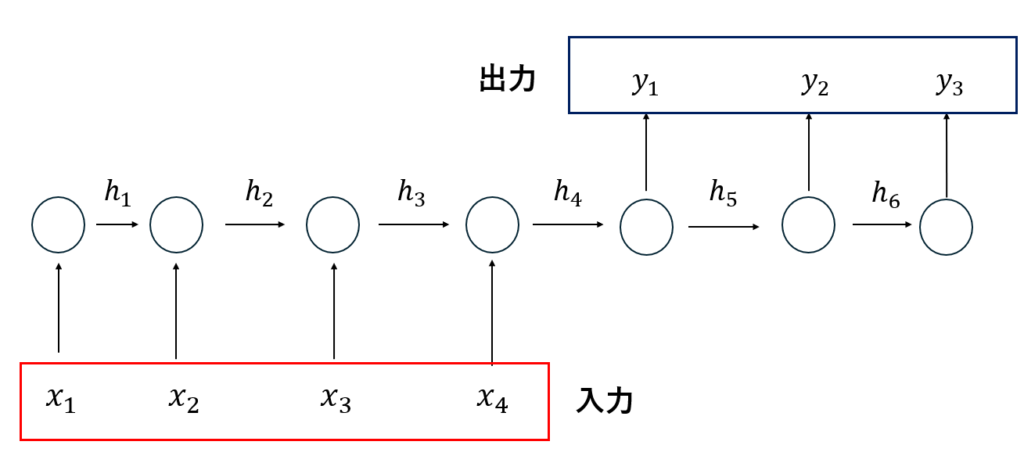
今回はリカレントニューラルネットワークの中でも最も基本的である単純リカレントニューラルネットワークについて解説していきます。下記の図がRNNの概要図になります。
リカレントニューラルネットワークは時系列ごとに入力(\(x_{t-1}\))と前時刻の情報(\(h_{t-1}\))を受け取り、出力(\(y_t\))と次の層へ伝える情報(\(h_t\))を生成します。前時刻の情報(\(h_{t-1}\))を伝える性質によって、過去の結果を考慮した解析が可能になるわけです。
もう少し細部を見てみましょう。
下記の図は入力(\( x_{t}\))と前時刻の情報(\( h_{t}\))をどのように処理して次の層へ伝える情報(\( h_{t+1}\))を生成するかを具体的に表したものです。式にすると\( h_{t+1} = tanh(W_h h_t + W_x x_{t} + b)\)となります。
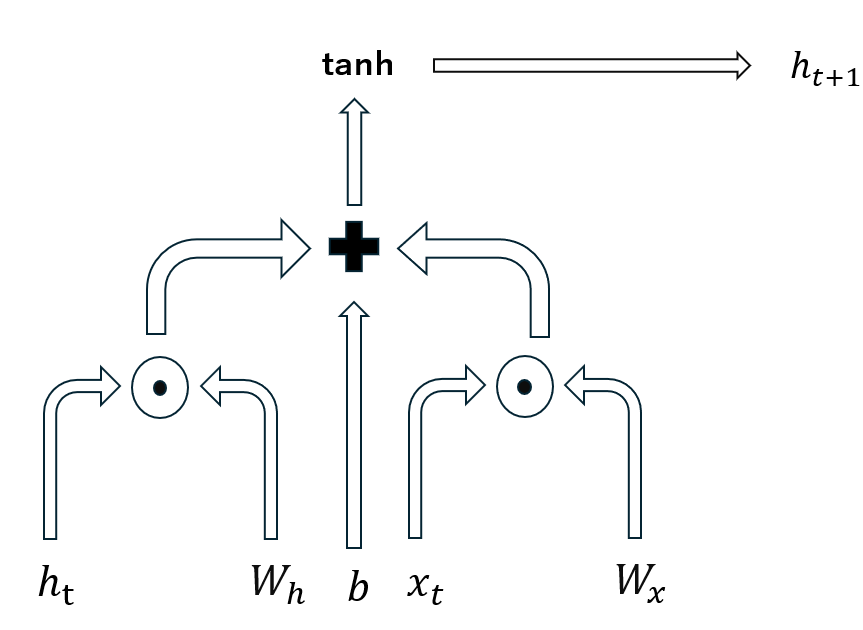
このようにして過去の情報を考慮した処理を実現しています。
単純リカレントニューラルネットワークの実装
単純リカレントニューラルネットワークの実装方法について解説していきます。
単純リカレントニューラルネットワークに必要な機能は大きく2つ分けられます。
- 重みやバイアスの定義
- ステップごとに中間層と出力の計算
SimpleRNNは単純な構造であるため、たったこれだけで実装できます。この方針に基づいてクラスを定義すると以下のようになります。
class SimpleRNN:
def __init__(self, units, input_dim, output_dim, activation='tanh'):
self.units = units
self.input_dim = input_dim
self.output_dim = output_dim
self.activation = tf.keras.activations.get(activation)
# 重みとバイアスの初期化
self.Wx = tf.Variable(tf.random.normal((input_dim, units), stddev=0.1), trainable=True)
self.Wh = tf.Variable(tf.random.normal((units, units), stddev=0.1), trainable=True)
self.bh = tf.Variable(tf.zeros((units,)), trainable=True)
self.Wy = tf.Variable(tf.random.normal((units, output_dim), stddev=0.1), trainable=True)
self.by = tf.Variable(tf.zeros((output_dim,)), trainable=True)
def call(self, inputs):
batch_size = tf.shape(inputs)[0]
h = tf.zeros((batch_size, self.units)) # 初期の隠れ状態
# 時間ステップごとに計算
for t in range(inputs.shape[1]): # time_steps
x_t = inputs[:, t, :] # 現在の時間ステップの入力
h = self.activation(tf.matmul(x_t, self.Wx) + tf.matmul(h, self.Wh) + self.bh)
# 出力層
output = tf.matmul(h, self.Wy) + self.by
return output次に実際にこのモデルを学習させて性能をテストしてみましょう。
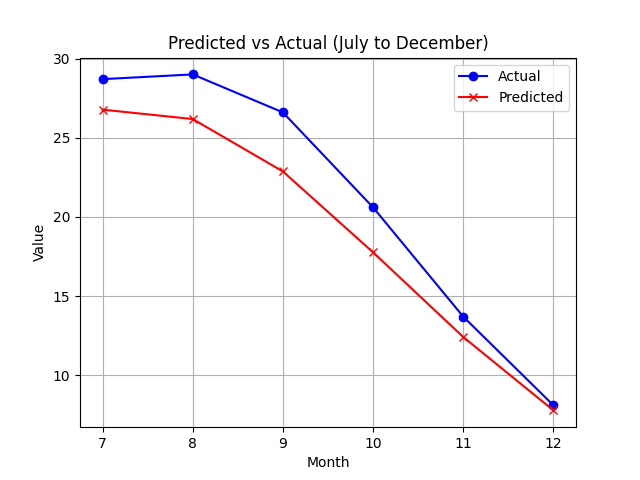
下記は先ほど作成した単純リカレントニューラルネットワークに2015~2023年までの各月の平均気温の変動を学習させて、入力データとして2024年の1~6月までの平均気温を与え、7~12月までの平均気温を予想するタスクを与えたものです。結果は以下のようになりました。
8月以降急激に気温が下がるという傾向を学習できていることが分かると思います。
まとめ
今回は時系列データに強みを持つRNNについて基本的な構造から実装まで解説しました。特に今回紹介した単純RNNはLSTMなど現在使用されているモデルの原点となっているモデルなのでぜひ覚えていてください。