データ拡張とは元データを改変してデータを増やす手法であり、データ不足の解決や汎化性能、ロバスト性の向上につながります。画像データの拡張の手法の一つとしてガウシアンノイズを付与する手法があります。本記事では、この手法について詳しく解説します。

1. ガウシアンノイズについて

ガウシアンノイズとはガウス分布（正規分布）に従う確率密度をもつノイズです。自然界には様々なノイズがあり、画像を撮影するセンサーや電気信号処理の際にもノイズが混入することがあります。このような実世界のノイズの多くはガウス分布で近似できるため、ガウシアンノイズを人工的に付与した画像で学習することで、より現実的な条件に対応できるロバストなモデルを構築できます。

ノイズが従うガウス分布は以下のような関数で表されます。

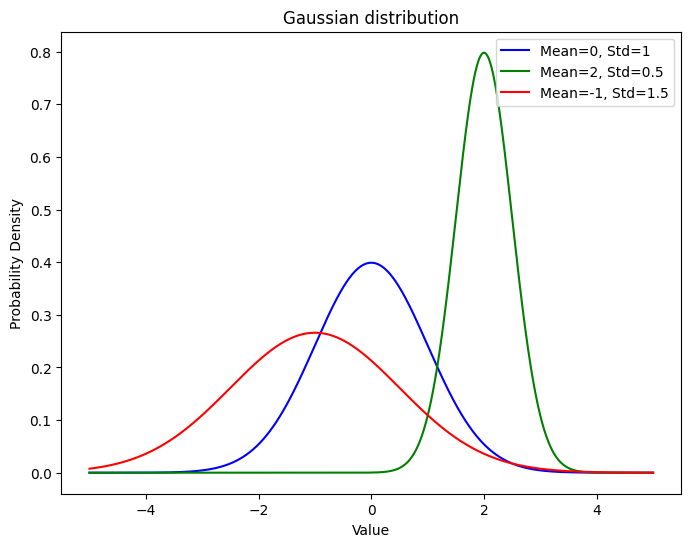
3種類の分布を表示してみました。横軸に \(x\) の値、縦軸に確率密度 \(f(x)\) の値を表示しています。 また、青で表されるものが \(\sigma=1,\mu = 0\) の正規分布を表しています。

2. ガウスノイズを画像に加えてみる

では実際に画像にガウシアンノイズを加えるとどのようになるのかを試してみましょう。標準偏差（σ）と平均値（μ）を様々に変更して実験を行いました。

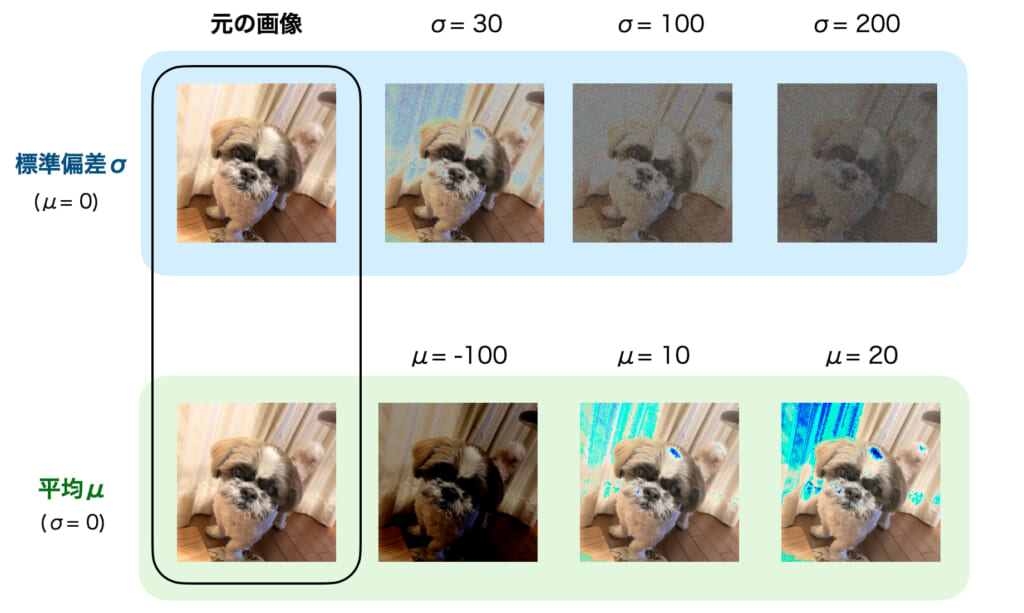
標準偏差（σ）の影響：標準偏差を大きくすると、砂嵐のようなノイズがより強く現れることが確認できます。これは、ノイズの振幅が大きくなるためです。

平均値（μ）の影響：平均値を変更すると、画像全体の明度が変化します。正の平均値では明るく、負の平均値では暗くなります。

色の変化について：ガウシアンノイズは各色チャンネル（RGB）に独立して適用されるため、局所的に特定の色が強調される現象が起こります。例えば、青チャンネルに大きな正のノイズ値が加わった部分は青みがかって見えます。これはランダムな現象であり、実行のたびに異なる色が強調される可能性があります。

3. 実装コード

最後に実装のコードを置いておくのでガウシアンノイズの標準偏差や平均値を変えて遊んでみてください。こちらは別画像での実装になっています。

# 必要なライブラリの読み込み

import numpy as np

import cv2

import matplotlib.pyplot as plt



# シードの設定

np.random.seed(42)



#ノイズ付与の関数

def add_noise(img, mu=0, sigma=1):

    # 画素数xRGBのノイズを生成

    noise = np.random.normal(mu, sigma, img.shape)

    # ノイズを付加して8bitの範囲にクリップ

    noisy_img = img.astype(np.float64) + noise

    noisy_img = np.clip(noisy_img, 0, img.shape[0]).astype(np.uint8)



    return noisy_img



# 画像の読み込み

img = cv2.imread('/mnt/lib/ztodataset/cnn/rcnn/009121.jpg', cv2.IMREAD_COLOR)



# 画像にノイズを追加

mu = 0

sigma = 100

noisy_img = add_noise(img, mu, sigma)



# 画像の表示

plt.subplot(1,2,1)

plt.imshow(img)

plt.title('raw image')

plt.xticks([])  

plt.yticks([])



plt.subplot(1,2,2)

plt.imshow(noisy_img)

plt.title(f'add noise mu{mu}_sigma{sigma}')

plt.xticks([])  

plt.yticks([])  



plt.tight_layout()

plt.show()

まとめ

ガウシアンノイズを用いたデータ拡張は、機械学習モデルの汎化性能を向上させる効果的な手法です。適切なパラメータ設定により、実世界の様々なノイズ条件に対応できるロバストなモデルを構築することができます。ぜひ様々なパラメータで実験し、その効果を確認してみてください。