LSTM(Long Short-Term Memory)はリカレントニューラルネットワーク(RNN)の一種で、長期的な依存関係を学習するために設計されたモデルです。通常のRNNが持つ「勾配消失問題」を克服するために開発され、時系列データや自然言語処理など、時間的な依存関係が重要なタスクに広く使われています。
RNNについて
まず、LSTMが登場する以前のRNNはどういうモデルだったか思い出しましょう。シンプルに表すと、次のような形になります。
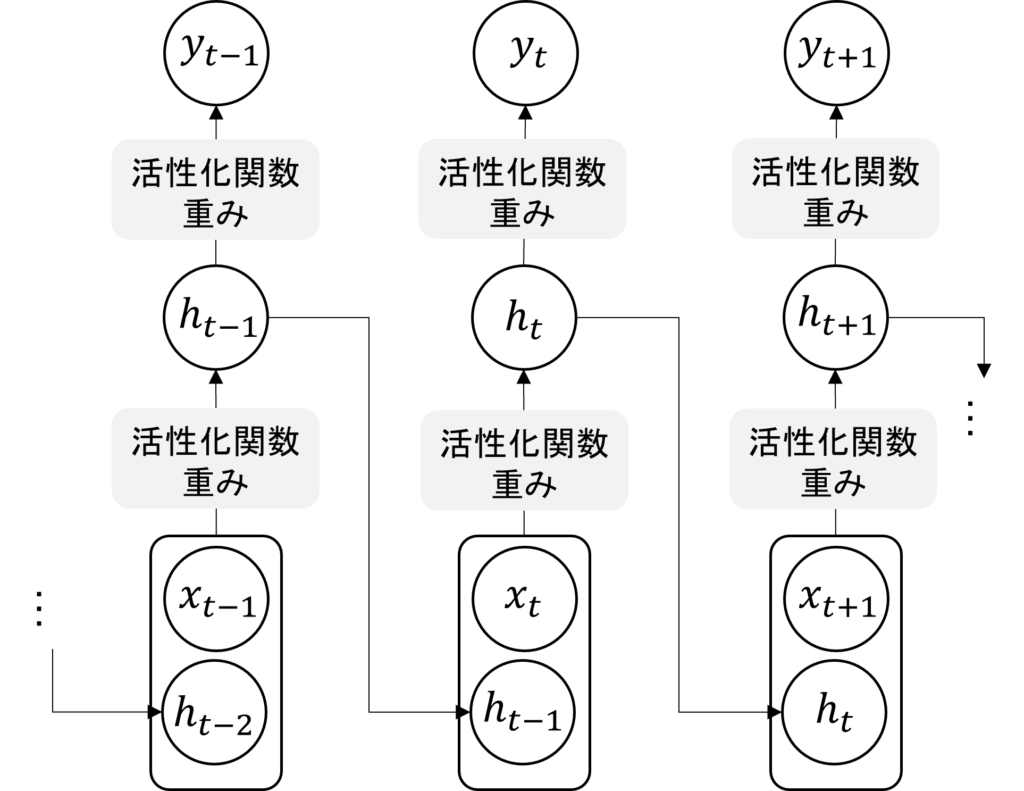
現在の時刻(ステップ)をtとし、入力系列データのうち現在時刻の入力を\(x_t\)、隠れ層出力を\(h_t\)、予測値を\(y_t\)と置いています。
RNNでは現在の入力と1時刻前の隠れ層出力を用いて現在の隠れ層出力を求めるため、
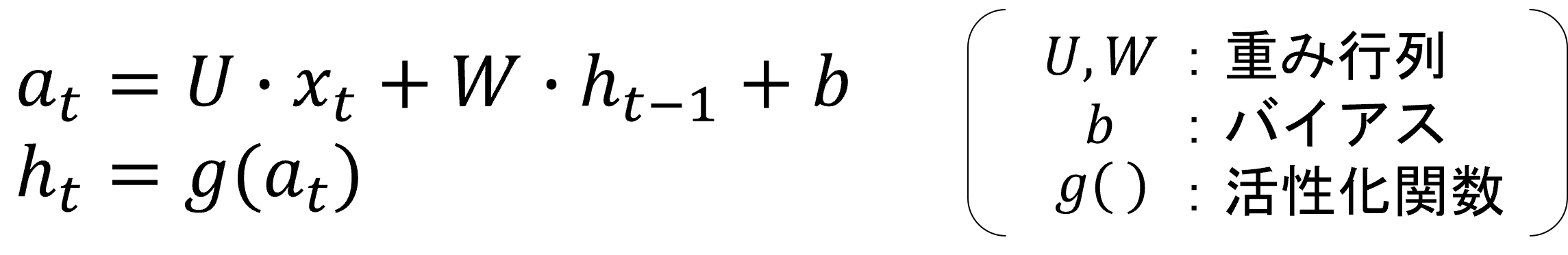
という計算を行います。
通常のRNNでは、1時刻前の隠れ状態を取り入れるだけなので、系列内で離れた位置にある要素同士の関係性(長期依存性)を学習するのが苦手です。下記のように誤差逆伝播を繰り返す過程で過去の情報に関する勾配が消失してしまうため、離れた要素同士の関係をうまく学習できないわけです。
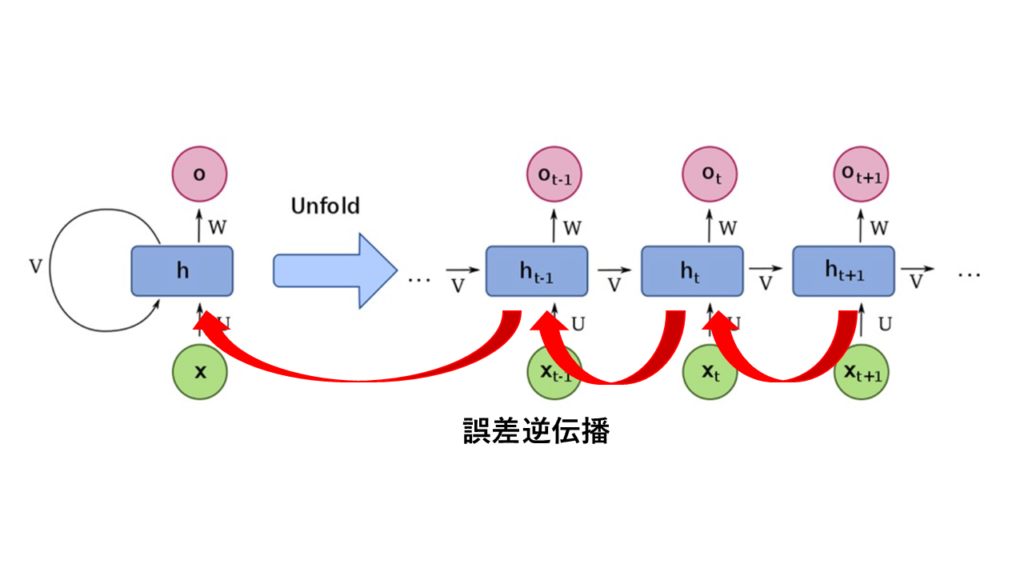
LSTM
LSTMは、先ほど述べたRNNの欠点を克服できるように設計されています。具体的には前の時刻に関する情報を送る過程に大きく分けて2つの要素が追加されており、これらを合わせてLSTMブロックと言います。
一つずつ分けて説明します。
CTC
一つ目は次の図の通り、\(h_t\)を計算する前の状態を保存しておくためのCTC(セル)です。\(h_t\)と異なる点は中間層の出力ではなく、これまでの時刻の情報を持つためのブロックであるという点です。各CTC間は主に加算関係にあるため、明確に過去の情報の取捨選択が得きるようになります。詳しくはゲートにて解説します。
※時刻tのみLSTMブロックの中身を記載し、t-1とt+1については省略しています。
※\(h_t\)から\(y_t\)を求める部分は通常のRNNと同じなので省略しています。
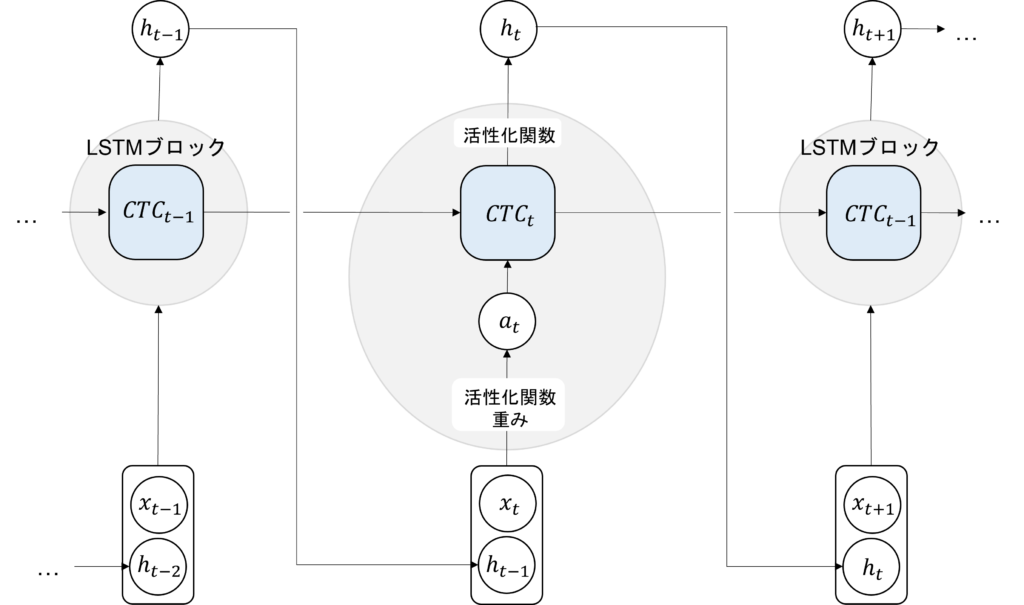
まず、通常のRNNと同じように\(x_t\)と\(h_{t-1}\)から以下の計算を行います。
(※通常のRNNではこれがそのまま\(h_t\)でしたが、ここでは\(a_t\)と置きます。)
\(a_t\)はRNNと同様に前の層の出力と入力を合わせたものになります
これに、1時刻前のCTCの値も足し合わせて現在のCTCを計算します。
あとは、\(CTC_t\)の値を活性化関数に通すことで、隠れ層出力\(h_t\)が得られます。
ゲート
2つ目は、値をどれくらい加えるかを決めるゲートです。このゲートによってCTC間の値を調節することができます。
LSTMには次の3つのゲートがあります。

つまり、それぞれネットワーク内の次の位置に存在します。
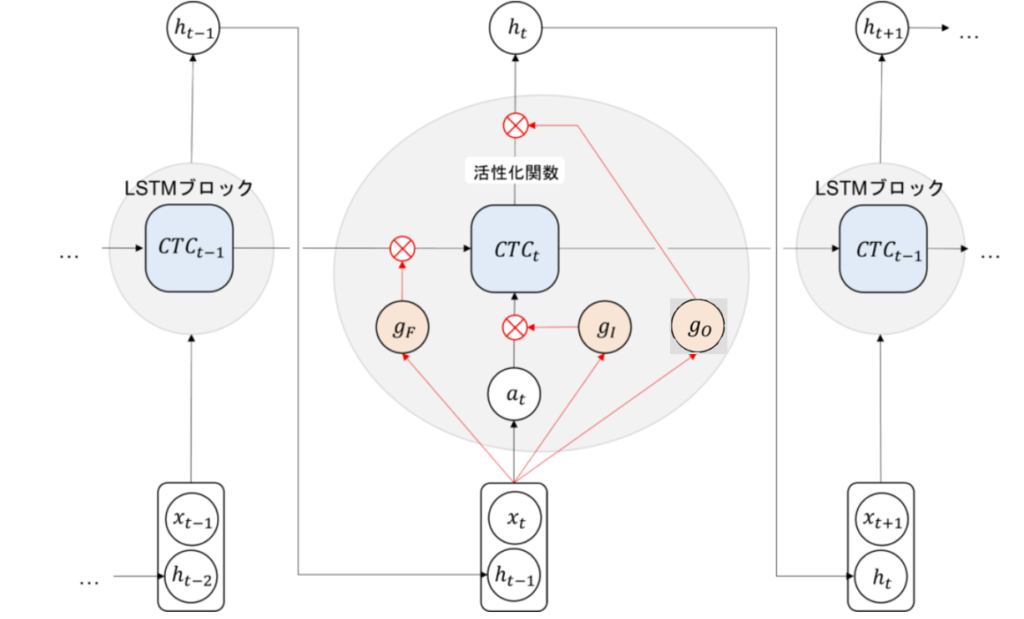
ゲートの値は、\(a_t\)と同じように\(x_t\)と\(h_{t-1}\)に重みをかけて足し合わせたものを、シグモイド関数に通して計算されます。つまり、値は0~1の範囲になります。
これを次のように\(a_t\)や\(CTC_t\)に要素ごとに掛け合わせる処理を行います。
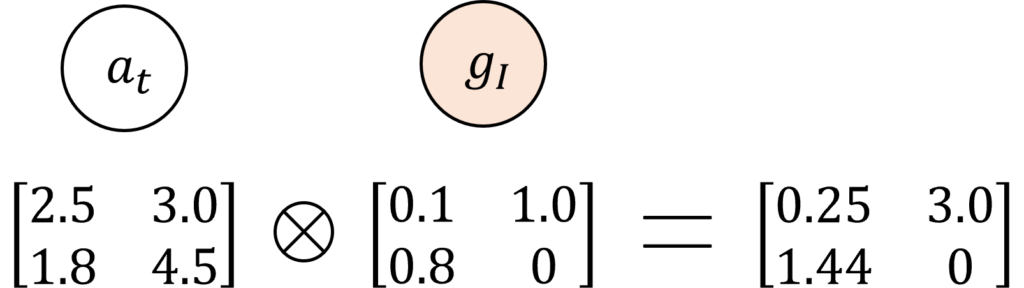
すなわち、ゲートの値が1に近い要素は残り、0に近い要素はなくなるといった具合に、後ろに伝える値を調整しているのです。
このゲート機構によって、各CTCについて取捨選択が可能になり、離れた位置の情報を長期間保持したり、適切なタイミングで減らしたりすることができるため、長期依存性を学習できます。
Pythonでの実装
LSTMの構造
pythonでLSTMの処理を実装すると以下のようになります。
下記はLSTMの1stepの計算を関数にしたものです。つまり、前の層の\(CTC_{t-1}\)と入力\(X_t\)を与えられ、それらを処理して、\(CTC_{t}\)と出力\(h_t\)を計算します。
この関数を連続的に呼び出すことでLSTMを実現できます。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数とtanh関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def tanh(x):
return np.tanh(x)
# LSTMの1ステップ計算
def lstm_forward(x_t, h_t_minus_1, c_t_minus_1, W_f, W_i, W_c, W_o, b_f, b_i, b_c, b_o):
# 入力と隠れ状態の結合
concat = np.hstack([x_t, h_t_minus_1])
# 忘却ゲート
f_t = sigmoid(np.dot(concat, W_f) + b_f)
# 入力ゲート
i_t = sigmoid(np.dot(concat, W_i) + b_i)
# セル候補
c_hat_t = tanh(np.dot(concat, W_c) + b_c)
# セル状態の更新
c_t = f_t * c_t_minus_1 + i_t * c_hat_t
# 出力ゲート
o_t = sigmoid(np.dot(concat, W_o) + b_o)
# 隠れ状態の更新
h_t = o_t * tanh(c_t)
return h_t, c_t実際に使ってみよう
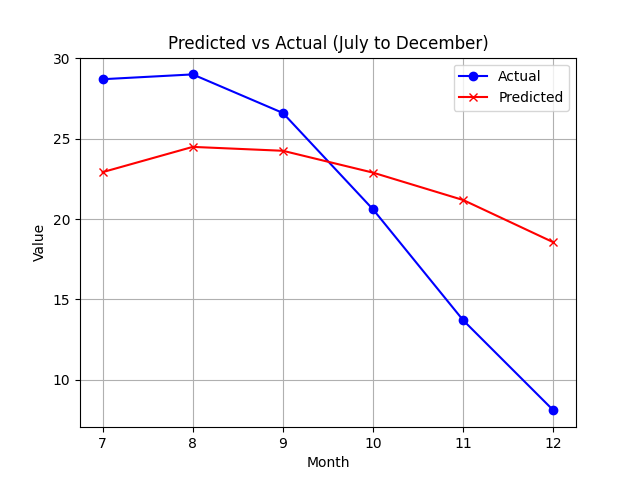
下記は先ほど作成したLSTMに2015~2023年までの各月の平均気温の変動を学習させて、入力データとして2024年の1~6月までの平均気温を与え、7~12月までの平均気温を予想するタスクを与えたものです。結果は以下のようになりました。
図のように、8月以降気温が下がっていくという傾向を学習できているのが分かると思います。このようにLSTMは時系列データに関するタスクを得意とするモデルです。
応用実装
LSTMの順伝播をより簡単に実装する方法を紹介します。
実装にあたって、現時刻の入力と1時刻前の隠れ層出力、そして3つのゲートと\(a_t\)の計算に使う重みとバイアスを、次のように行列にまとめて計算すると実装がシンプルになります。
(図中の「×」は行列積です。)
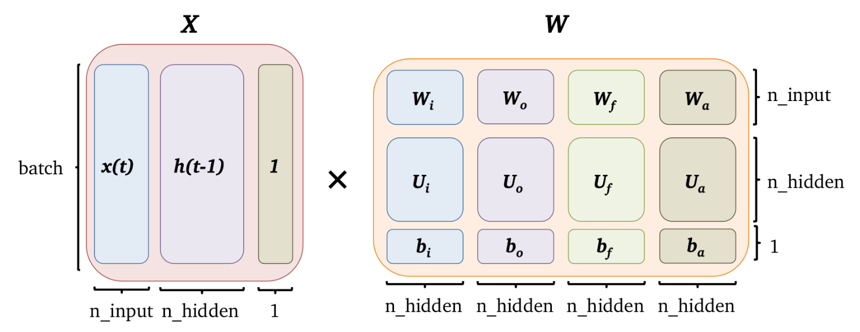
このように計算すると、行方向にはミニバッチのデータ、列方向には入力ゲート、出力ゲート、忘却ゲート、\(a_t\)の値(それぞれ活性化関数に通す前)が並んだ行列が得られます。
よって、それを列方向に4つに区切った後活性化関数に通します(ゲートはシグモイド関数、\(a_t\)はtanh関数)。
これをPythonで書くと、以下のようになります。
まとめ
今回はRNNの中でも長期依存関係に強いLSTMの仕組みについて解説しました。LSTMは実際の研究などでも盛んに使われてる技術なのでぜひ覚えてみてください。