Contents
機械学習におけるダイバージェンスの必要性
機械学習では確率分布を扱うことが多く、確率分布同士の差異を計りたくなることも多いです。例えば代表的な生成モデルであるVAE(変分オートエンコーダ)では、潜在変数の分布を正規分布に近づけるように学習させるため、損失関数に分布誤差の項が現れます。また、強化学習においてもTRPO(Trust Region Policy Optimization)やPPO(Proximal Policy Optimization)といった手法では、更新前と更新後の方策が変化しすぎないようにそれらの誤差を小さく抑えるように学習させたりします。そのようなときに使われるのがダイバージェンスやエントロピーなどといった概念です。よって今回はダイバージェンスやエントロピーといった、二つの確率分布の差異を計る尺度についてまとめます。
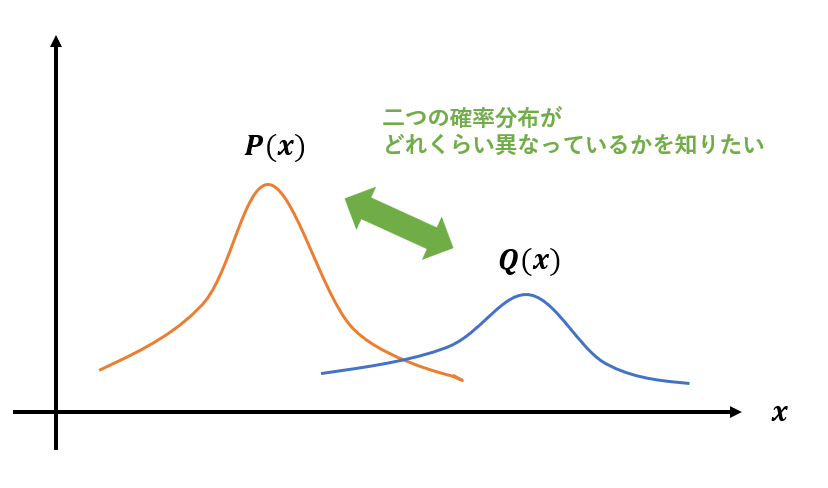
2つの確率分布の差異を計る尺度
確率分布の差異を計る尺度としては、主にダイバージェンスがあります。2つの関数\(p(x)\)と\(q(x)\)について\(D(p,q)\)が以下の2つの条件を満たすとき、\(D(p,q)\)はダイバージェンスと呼ばれます。
- \(D(p,q) \geqq{0}\)
- \(D(p,q) = 0 ⇔ p(x) = q(x)\)
この定義自体はそんなに重要ではないですが、ダイバージェンスには様々な種類があり、機械学習でよく用いられるものは覚えておくべきでしょう。有名なものとして、
- KLダイバージェンス
- クロスエントロピー
- JSダイバージェンス
- L2ダイバージェンス
- べき密度ダイバージェンス
などがあり、今回はこれらを紹介します。
KLダイバージェンス (Kullback-Leibler Divergence)
まず最もよく用いられるのではないかと思われるダイバージェンスの一つがKLダイバージェンス(Kullback-Leibler Divergence)です。
真の確率分布P(x)、予測確率分布Q(x)のKLダイバージェンス\(D_{KL}(P, Q)\)は、
と表されます。この式の意味は確率同士の差を取って期待値としての和を取ったという感じです。ちゃんと二つの分布が同じときは0になり、KLダイバージェンスが大きいほど二つの確率分布の差が大きいということになります。
ちなみにP(x)やQ(x)はxが離散的なときの確率分布と仮定しています。xが連続的なときの確率分布は積分を使って表す必要があります。
クロスエントロピー
クロスエントロピーも確率分布の差異を表す有名な評価指標で、機械学習の損失関数でもクロスエントロピー誤差としてよく使われます。クロスエントロピーH(P, Q)は、真の確率分布P(x)、予測分布Q(x)に対して以下のように定義されます。
ちなみに、クロスエントロピーは以下のようにKLダイバージェンスを使って書くこともできます。
ここで、H(P)は確率分布Pのエントロピー(今回はエントロピーについては詳しく解説しません)です。つまりKLダイバージェンスは、実はクロスエントロピーと真の分布のエントロピーとの差を表しているわけですね。
JSダイバージェンス (Jensen-Shannon Divergence)
KLダイバージェンスは非常によく用いられている指標ですが、対称性がありません。つまり、
が成立しないです。そこで、対称性を持つ指標としてJSダイバージェンス(Jensen-Shannon Divergence)というものが登場しました。JSダイバージェンスの定義は
と表されます。JSダイバージェンスは対称性が成り立ちます。
L2ダイバージェンス
KLダイバージェンスほど使われてはいませんが、二つの確率分布の距離(L2ノルム)に基づいた手法としてL2ダイバージェンスがあります。L2ダイバージェンスは以下の式で表されます。
L2ノルムの計算方法とほぼ同じですね。ちなみにこちらも対称性があります。誤差測定としての使われ方が多いようです。
べき密度ダイバージェンス (Power Divergence)
べき密度ダイバージェンスはβダイバージェンスとか呼ばれることもあるらしいです。βという任意のパラメータを導入しているのが特筆すべき点であり、βの値を変えることで様々なダイバージェンスの定義式に変化するという特徴があります。つまり、KLダイバージェンスなどの一般化された拡張版という感じです。べき密度ダイバージェンス\(D_{pow}\)は、以下の式で表されます。
ただし、\(\beta\)は正で、これはxが連続的な場合です(離散的な場合の式は調べても見つからなかったため、載せませんがxを離散的にするだけなので導出はやればできるはず)。
式を見ると、\(\beta\)が1のときはxが連続な場合のL2ダイバージェンスになることがわかります。他にも、β→0の極限を取ると上手いこと拡張版のKLダイバージェンスになったりと様々な既存のダイバージェンスを再現できます。
まとめ
今回は機械学習で用いられる、確率分布同士の差異を計る尺度についてまとめました。結構機械学習で確率分布の差異を求めたい場合は多いので、覚えておくとよいでしょう。