機械学習における最適化とはパラメータを調節することで、ある特定の目的に
最適な関数やモデルを設計することを意味します。
パラメータの調整とは損失関数が小さくなるように重みを変更することです。
具体的には図のように損失関数\(L\)を小さくするために\(w\)で微分することで\(L\)を小さくするために必要なベクトルが得られます。(誤差伝搬)
。
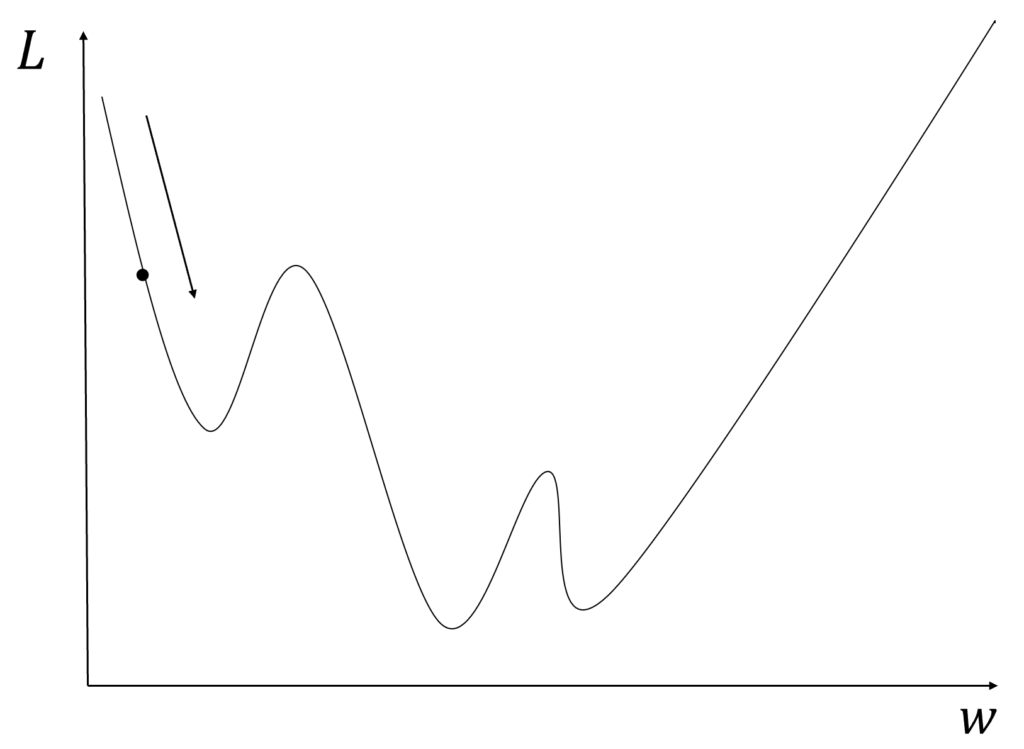
詳しくはこちらをご覧ください
勾配降下法
勾配降下法は1800年代に開発された手法で関数の最小値を求めるために編み出されました。
勾配降下法はすべての学習データに対して損失関数の偏微分を計算します。
具体的には、誤差伝搬によって各パラメータ\(\theta_{i}\)に対して損失関数を偏微分したものを計算します。
計算された偏微分はLを大きくする方向への変化量であるため、偏微分した値を元のパラメータから引くことでLを小さくする方向にパラメータを動かします。
こうすることで損失関数が小さくなるように各パラメータが変更されるわけです。また変化量も偏微分に依存しますが偏微分をそのまま引いた場合に変化が極端すぎることがあるため学習率 \(\alpha\)をかけることで変化量を調節します。学習率は大きすぎても小さすぎてもよくないです。このパラメータの更新を複数回行うことで損失関数を小さくする重みになるように調整していきます
学習率が小さい場合最小値ではなく局所解で値が動かなくなります
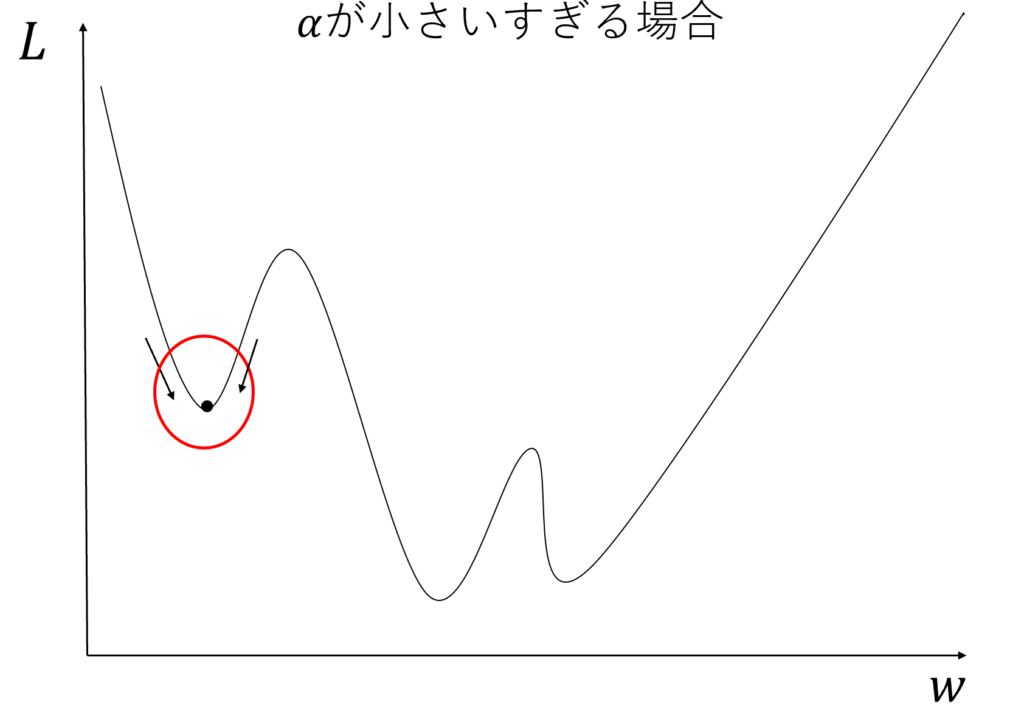
学習率が大きすぎる場合には値が変わりすぎて収束しなくなります。
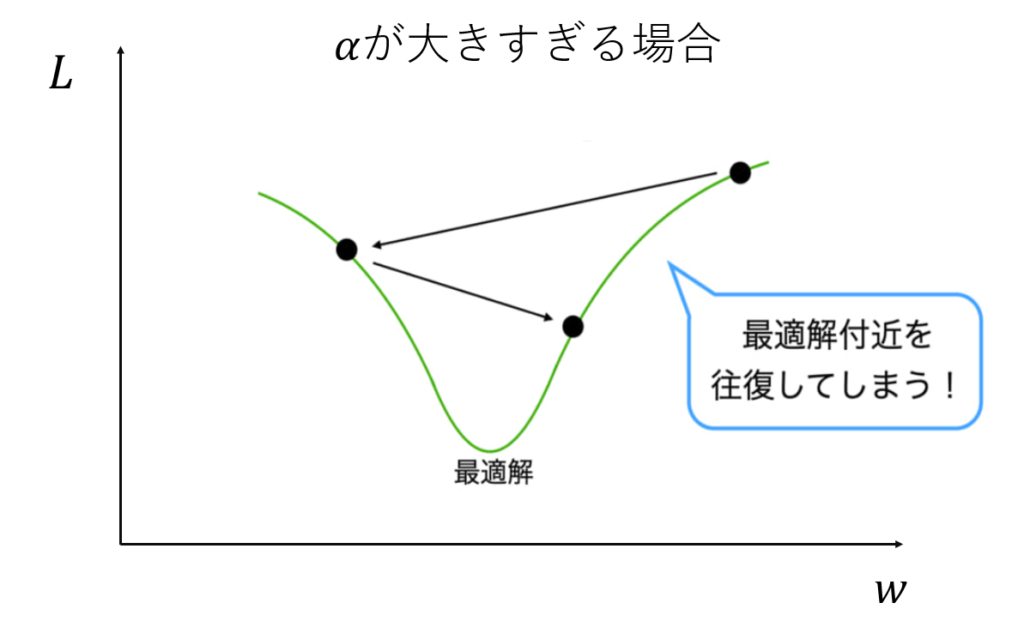
SGD(確率的勾配降下法)
SGDは1950年代に開発された手法で大規模なデータのために作られました。
SGDは学習データが大規模な場合に使用されます。学習データが大規模な場合には、すべてのデータに対して勾配を計算する場合に多くの計算量が掛かってしまいます。そこですべてのデータではなくミニバッチと呼ばれるランダムにデータを取り出した小規模なデータを複数個作成し、それらに対して勾配降下法を繰り返すことで効率よく学習を進めます。
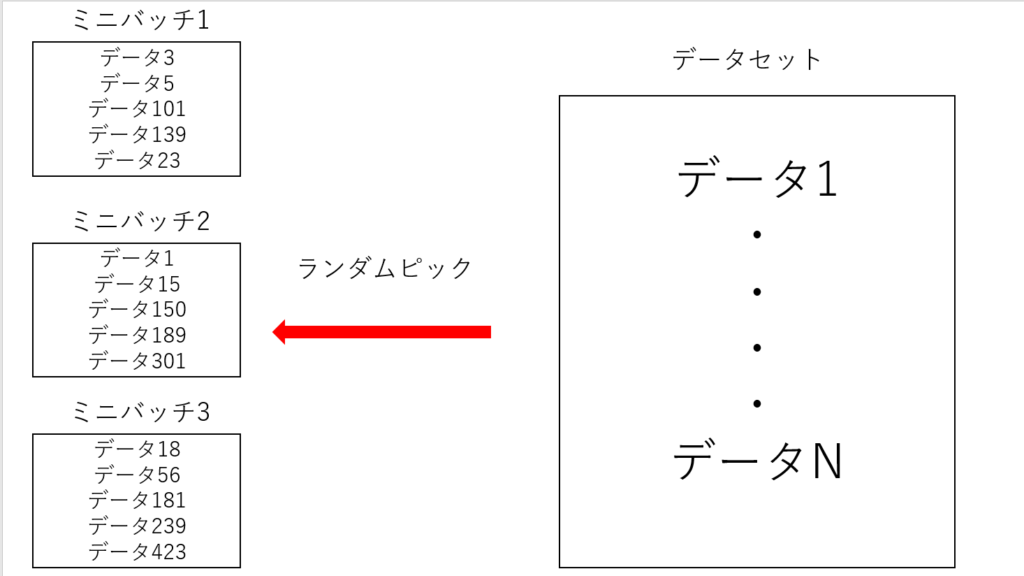
Momentum
Momentumは1990年代に開発された手法でSGDを改良して鞍点を抜け出すために編み出された手法です。
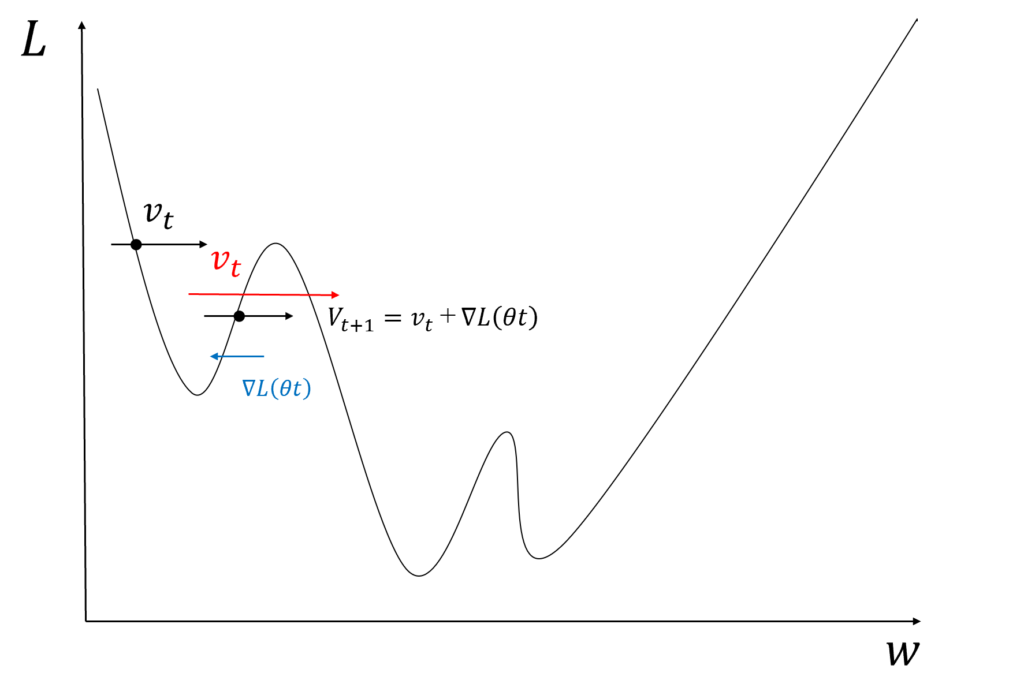
Momentumでは更新について前回の更新が影響を与える仕組みになっています。Momentumの式は以下のようになります。
これは物理の慣性力を模したものであり、更新に一貫性が出ることによって局所解での往復などが起こりにくくなりSGDより早く収束できるようになります。
図のようにSGDのように損失関数のみで重みを変更する場合は局所解によって複数回谷を往復する可能性が高いですがMomentumの場合は図のように前回の変化量が慣性によってある程度残るため谷を越えやすくなります。
AdaGrad
AdaGradは2011年に開発された手法でこちらもSGDを改良したものになります。
AdaGrad の特徴は、これまでの更新量に応じて、各パラメータごとに更新量を減少させる学習方法です。式は以下のようになります。
このように、更新量がhに蓄積されていくため、だんだんと更新量が小さくなっていきます。これにより、全パラメータの変化量が安定しすることで、学習も安定します。
RMSProp
RMSPropは2012年に開発された手法でAdaGradを改良したものです。AdaGradは長期間の学習においては勾配が極めて小さくなるという問題に対処したものです。
RMSPropもAdaGrad同様に各パラメータごとに更新量を変化させます。式は以下のようになります。
RMSPropは勾配の急激な変動や緩やかな変動に対して、適切な学習率を設定できます。
\(\gamma \)は通常0.9ほどに設定されます
\(E[g^2]_t\)の更新式からわかるように過去の勾配の二乗の移動平均を減少させ最新の勾配の二乗を足すことで更新されています
そのことから、現在の勾配が大きい場合は学習率は小さくなります。これによってパラメータが一気に更新され値が最適解から遠く離れてしまうことを防げます。
現在の勾配が小さい場合は学習率が大きくなります。これにより、勾配が緩やかな場合にも変化量が大きくなるため収束が速くなります。
このようにRMSPropは現在の勾配に依存して学習率を調節するため学習を安定させることができます。
Adam
Adamは2014年に開発された手法でRMSPropやMomentumの利点を組み合わせた最適化アルゴリズムです。
勾配の平均と分散の両方を利用して計算します。式は以下のようになります。
平均と分散を組み合わせることでより収束速度と安定性が上がります。
Momentunの前の移動の方向によって学習を促進させるという特徴にRMSPropの変化量の大きさによって学習量を調節する仕組みを組みわせたことで方向と移動量の両方から調節できるわけです。
比較してみよう
乳がんに関するデータセットに対してMLPのTrainに対する精度の変化からそれぞれの特徴を再確認しましょう
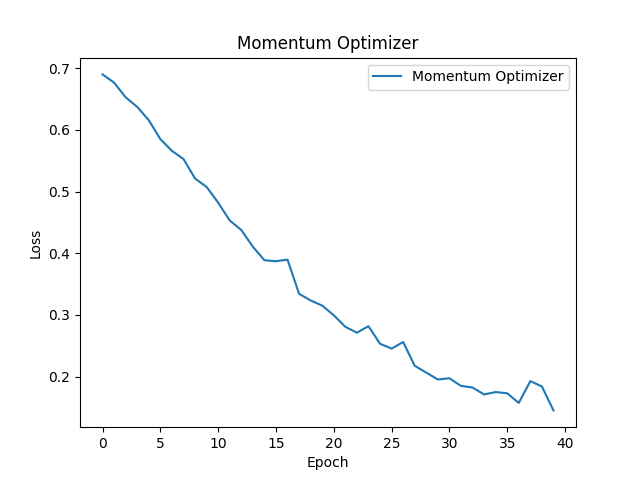
下記はMomentumによるモデルの精度変化です。比較的なめらかに誤差が小さくなっていることがわかると思います。これはMomentumは発振しづらい性質によるものだと考えられます。
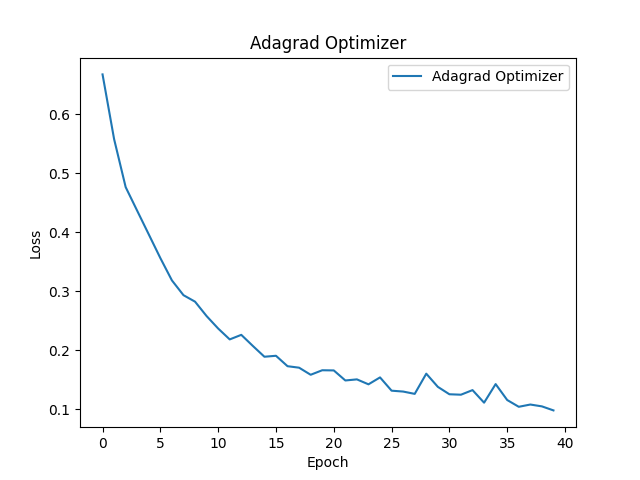
下記はAdaGradによるモデルの精度変化です。最初は急速にだんだん変化が小さくなっていると思います。これはAdaGradが勾配の蓄積により学習率がだんだん小さくなるためです。
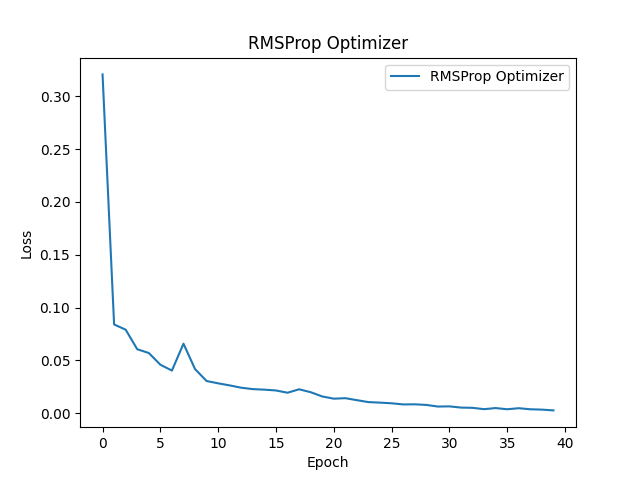
下記はRSMPropによるモデルの精度変化です。最初の変化は急速ですが以降一定の変化を見せています。これはRSMPropが勾配の変化量に合わせて学習率を変化させるため比較的一定の速度で変化していきます。
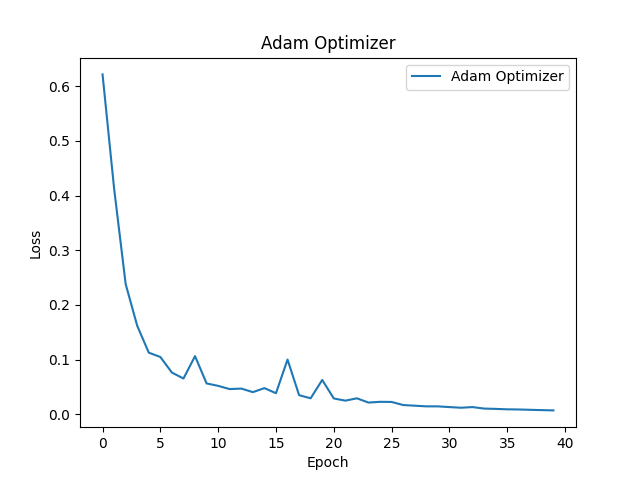
下記はAdamによるモデルの精度変化です。MomentumとRSMPropの両方の性質を持つことから比較的滑らかに変化し、収束速度も一定です。
その他の最適化手法
ここでは上記で説明した最適化手法をさらに改善したものを紹介します。細かい式の解説などは行いませんが最新のものがどれほどが是非体感してみてください。
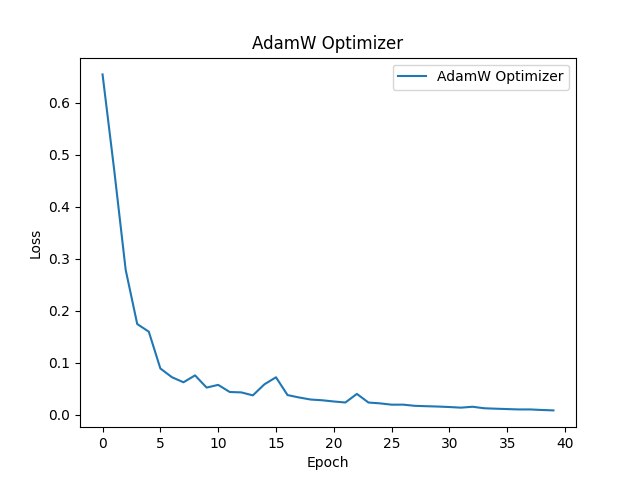
AdamW
下記はAdamWという最適化手法を使用したものです。AdamWはAdamを改善したものでより安定した学習を行えます。実際にAdamと比較してかなり滑らかな学習曲線を描いていると思います。また過学習を抑える工夫もされており非常に実用的な手法です。
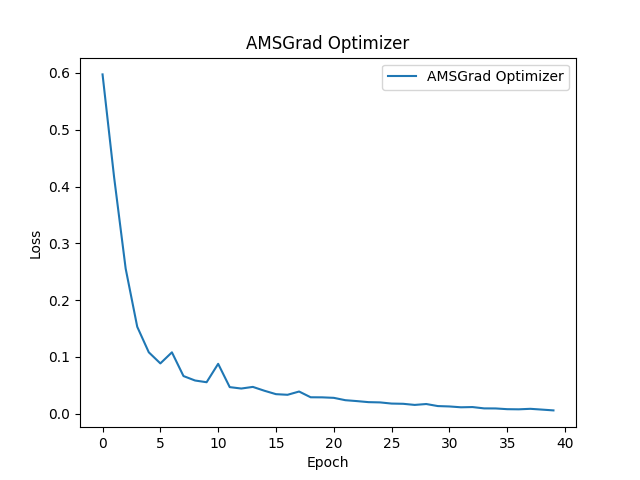
AMSGrad
下記はAMSGradという最適化手法を使用したものです。こちらも同様にAdamを改善したものになります。AMSGradは実装も比較的簡単でありより安定した学習を可能にします。
まとめ
今回は機械学習モデルの最適化手法を紹介しました。最適化はモデルの性能を直接左右するため非常に重要です。是非マスターしてください。