回帰分析には線形回帰、ロジスティック回帰など様々な方法がありますが、今回はあまり有名ではない順序回帰について解説します。
本記事は回帰分析がどのようなものかは大体ご存じの方を対象としています。
そもそも回帰分析とは
回帰分析は説明変数(要因となるデータ)と目的変数(結果)との関係をモデル化する分析手法です。つまり、調べたいデータ間の関係を数式として表すことで、将来のデータの変動を予測したりすることができるようになるというわけですね。回帰分析にもいろいろ種類があり、一つの説明変数と一つの目的変数との関係を調べる単回帰分析や、複数の説明変数と一つの目的変数との関係を調べる重回帰分析、二値分類に使われるロジスティック回帰(回帰というより分類)などがあります。
順序回帰とは
順序回帰は、目的変数が順序変数である場合に使用される回帰分析手法です。順序変数というのは例えば、ある商品の評価を「とても良い」、「良い」、「悪い」、「とても悪い」のようにつけるスケールのように、ラベル間に順序はあるが数値の比率、差などはもたない変数のことです。そのため、順序回帰は分類と回帰の中間に位置します。分類でいいような気がするかもしれませんが、単純な分類とは異なり、ラベル間の順序を考慮することでより精度の高い予測を行います。
順序回帰には様々な手法がありますが、代表的なものは順序ロジスティック回帰と順序プロビット回帰という手法です。これらはいずれもカテゴリカルな順序変数の裏には連続的な潜在変数が存在する、という仮定に基づいています。すなわち、説明変数を潜在変数に変換した後、その潜在変数の値を閾値によって分類するということを行います。
順序ロジスティック回帰
まず、順序ロジスティック回帰について説明していきます。
前提として、通常のロジスティック回帰の知識が必要です。ロジスティック回帰は以下の図のように、説明変数からどのクラスに分類されるかの確率を計算するのでした。ほとんどの場合は目的変数が二値(0か1)のみを取る二項ロジスティック回帰です。
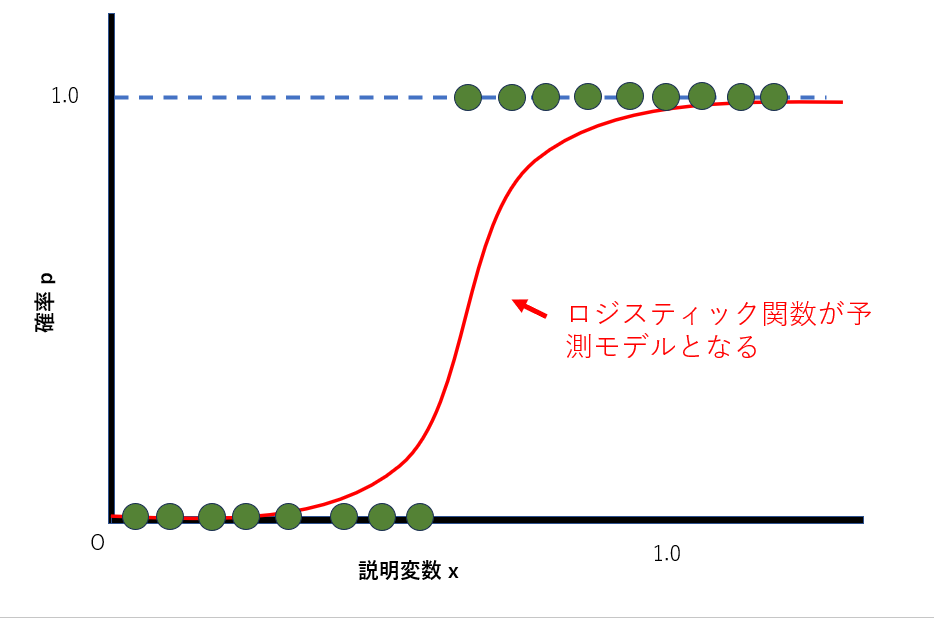
説明変数をx、目的変数をyとしたとき、yが0と1のうち1に分類される確率pは、ωをパラメータとしてxとpの関係を
と表せるのでした。これは
という変数y*をシグモイド関数に代入していると解釈することができます。より一般的には、βを回帰係数、εをロジスティック分布に従う誤差項として、
で表される潜在変数を閾値によって分類する問題がロジスティック回帰です。ここでは、閾値の値はハイパーパラメータとしてあらかじめ設定する必要があります。
一方、順序ロジスティック回帰の場合、閾値も学習過程で決定されるものとなります。ほとんどはロジスティック回帰と同じで、βを回帰係数、εをロジスティック分布に従う誤差項として、
と潜在変数を計算した後、潜在変数の値によってクラス分けを行います。y* < μ1ならクラス1、 μ1<y*<μ2ならクラス2、といった具合です。しかし、これらの閾値は学習によって決定されるもので、人間があらかじめ与えるものではありません。
これを数式で表すと、
- \(Y\):順序カテゴリに対応する応答変数
- \(j\):応答変数のカテゴリ
- \( \alpha_j\):カテゴリの閾値
- \(x\):説明変数(入力)
- \( \beta\):回帰係数
これをイメージとして表したものが下の図です(厳密にはこの図は正確じゃないです)。潜在変数の閾値により、どのクラスに分類されるかが決まります。
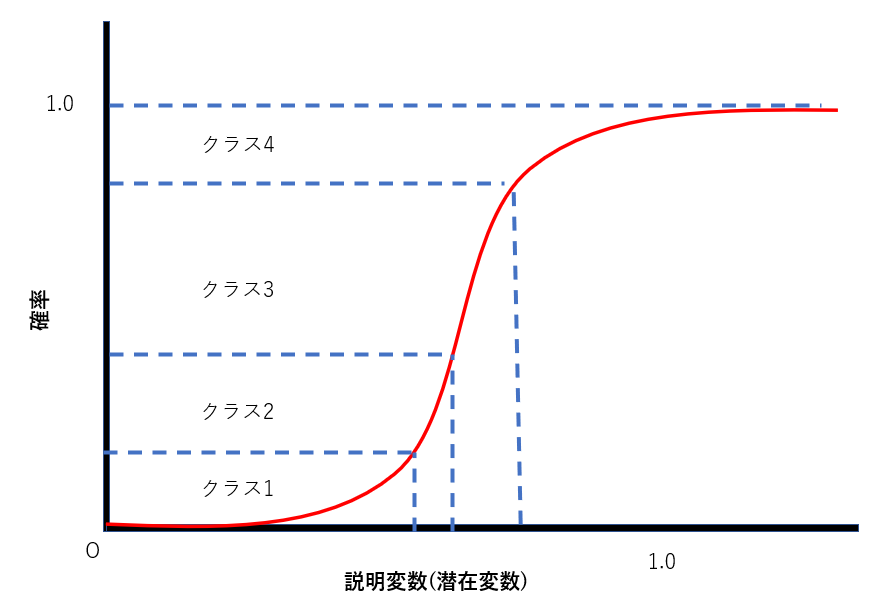
この図においてはクラス3に分類される確率が最も大きいため、クラス3に分類されると予測する、といった具合です。
順序ロジスティック回帰の実装
いろいろ実装のしようはあると思いますが、statsmodelsで公開されているOrderdModelというAPIを使うのが一番楽でしょう(参考)。statsmodelsはPythonで動く統計解析ソフトです。回帰分析もいろいろ使えます。
import pandas as pd
import statsmodels.api as sm
from statsmodels.miscmodels.ordinal_model import OrderedModel
# データの作成
data = {
'satisfaction': [0, 1, 2, 1, 0, 2, 2, 0, 1, 1],
'age': [22, 35, 28, 50, 45, 23, 41, 34, 36, 58],
'income': [2000, 3000, 2500, 5000, 4500, 2300, 4000, 3100, 3600, 4800]
}
df = pd.DataFrame(data)
# 目的変数と説明変数の定義
y = df['satisfaction']
X = df[['age', 'income']]
# 順序ロジスティック回帰モデルの定義
model = OrderedModel(y, X, distr='logit') #logitならロジスティック回帰、probitにすればプロビット回帰
# モデルのフィッティング
result = model.fit(method='bfgs')
# 新しいデータで予測
X_new = pd.DataFrame({
'age': [30, 40],
'income': [3500, 4200]
})
# 予測確率の計算
pred_probs = result.predict(X_new)
# 予測確率を表示
print("New data predictions:")
print(pred_probs)ここでは年齢と収入に基づいて10人の顧客の満足度を0、1、2の順序変数に分けています。
順序プロビット回帰
順序プロビット回帰はほとんど順序ロジスティック回帰と同じで、潜在変数
における誤差項εが正規分布に従う場合になっただけです。つまり、正規分布によって変動する潜在変数を閾値によってクラス分けするのが順序プロビット回帰というわけです。
順序プロビット回帰の実装
こちらもstatsmodelsで公開されているAPIを使って実装が楽です。順序ロジスティック回帰の実装の項を参照してください。
まとめ
今回は順序回帰について、とりわけ順序ロジスティック回帰及び順序プロビット回帰について解説しました。E資格試験においても問われる箇所なので、よく復習しておきましょう。